微分流形
微分流形
严格定义微分流形: 粗略地看, 微分流形就是带有微分结构的拓扑空间.
定义1: 拓扑空间(M, )称为n维微分流形(n-dimensional differentiable manifold), 如果M有开覆盖{}(M=), 满足
- 对每一个, 存在同胚(是上通常拓扑衡量的开子集);
- 若, 则是(光滑)的;
定义2: 坐标系()在数学上又叫图(chart) 满足定义1 条件1、2的全体图的集合{()}叫图册(atlas). 条件(2)又称相容性(compatibility)条件, 因此说一个图册中的任意两个图都是相容的.
定义3: 互相微分同胚(diffeomorphic to each other ), 如果, 满足
- 是的
- 是一一映射
记号: M上的所有光滑函数记为
切矢和切矢场
定义1: 映射 : 称为点 的一个 矢量(vector), 若 , 有
- (线性性);
- (莱布尼茨律), 其中代表函数 在p 点的值,亦可记作.
例1: 由上述定义立即可以得到p点的n个矢量, 记作.它们作用在任一函数的结果为:
它们被称为坐标基底
定理1: p点所有矢量的线性空间为, 应该有, 也就是:
其中被称为坐标分量
记号: 我们使用为一个坐标系, 其中是上的一个开集, 是一个向的映射
流形上的矢量场
定义2: 设 为流形的子集, 若给的每一个点指定一个矢量, 就得到一个定义在上的矢量场(vector field)
定义3: 两个光滑矢量场 (指) 的对易子是一个光滑矢量场, 定义为:
定理2: 任意一个坐标系的任意两个基矢场都互相对易
对偶矢量场
定义1: 是 上的有限维线性空间, 线性映射 称为上的 对偶矢量(dual vector). 上的全体对偶矢量集合称为的对偶空间, 记作.
例1: 假设上有基矢变换, 则相应的对偶矢量基地变换是什么呢?
假设我们有$, 那么:
其中表示矩阵的转置.
于是得到
最后给出:
例2: 微分算符诱导对偶矢量场, 记为.
设, 第 个坐标.可以看作一个函数,于是有它的微分, 由如上定义显然有:
一般的, 我们可以用这一组基底来分解:
其他问题
例1: 讨论极坐标中的坐标基矢, 它们是正交归一的, 但是不是坐标基底, 因为坐标基底有:, 其中. 所以此处.
记号:
抽象指标表示: 使用形如来表示存在一个(2,1)型张量.
讨论张量的分量时, 使用希腊字母作为具体指标, 展开式为
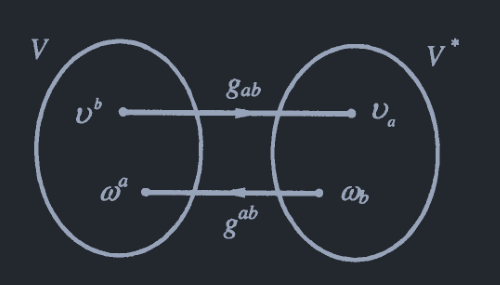
例: 因为度规, 所以应该记为. 设,则 , 在有度规时的一个自然的同构映射为. 应用上可以定义的对偶矢量. 写作:
类似的, 通过从的的逆映射, 因此我们可以看到是(2,0)型张量, 本来应该记作, 但是通常都简单记为. 表示上有: